MAKE A MEME
View Large Image
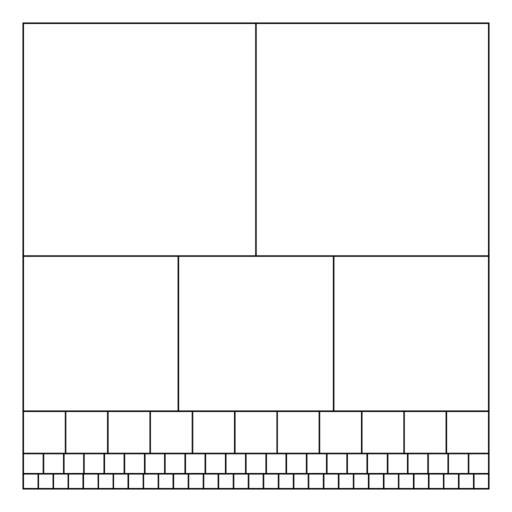
| View Original: | Znam-2-3-11-23-31.svg (396x396) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Znam-2-3-11-23-31.svg Graphical demonstration that 1 1/2 + 1/3 + 1/11 + 1/23 + 1/31 + 1/ 2×3×11×23×31 Each row of squares has k squares of side length 1/k for some k in the set 2 3 11 23 31 47058 ; for instance the first row has two squares of side length 1/2 Thus each row of squares has area 1/k and all six rows together exactly cover a unit square The bottom row with 47058 squares of side length 1/47058 would be too small to see in the figure and is not shown Sets of integers such that <math>1 \sum 1/x_i + \prod 1/x_i</math> such as the set 2 3 11 23 31 used to construct this figure correspond to solutions of Znám's problem As all numbers in the set 2 3 11 23 31 are prime their product 47058 is a primary pseudoperfect number en wikipedia 2006-12-05 David Eppstein wikipedia en File Sylvester-square svg David Eppstein original upload log page en wikipedia Znam-2-3-11-23-31 svg 2006-12-05 01 51 David Eppstein 256×256×0 5661 bytes <nowiki>Graphical demonstration that 1 1/2 + 1/3 + 1/11 + 1/23 + 1/31 + 1/ 2×3×11×23×31 Each row of squares has k squares of side length 1/k for some k in the set 2 3 11 23 31 47058 ; for instance the first row has two squares of sid</nowiki> Number theory Files by User David Eppstein from en wikipedia | ||||