MAKE A MEME
View Large Image
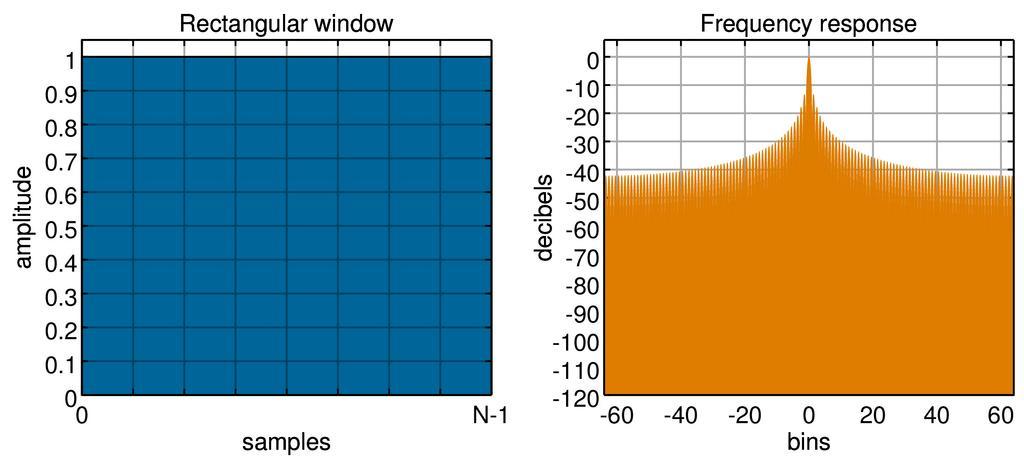
| View Original: | Window function (rectangular).png (2500x1123) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Window function (rectangular).png File Window function and frequency response - Rectangular svg rectangular window and frequency response own 2013-02-09 Bob K original version Olli Niemitalo Octave commands This script run in Octave generated the following images File Window function rectangular png File Window function hann png File Window function hamming png File Window function Tukey; alpha 3D 0 5 png File Window function sine png File Window function sinc or Lanczos png File Window function triangular png File Window function bartlett png File Window function gauss png File Window function bartlett-hann png File Window function blackman png File Window function Kaiser; alpha 3D 2 png File Window function Kaiser; alpha 3D 3 png File Window function and frequency response - Planck-taper epsilon 3D 0 1 png File Window function nuttall png File Window function blackman-harris png File Window function blackman-nuttall png File Window function flat top png File Exponential window and frequency response half window decay png File Exponential window and frequency response 60dB decay png File Window function and frequency response - Hann-Poisson alpha 2 png File Window function and frequency response - SRS flat top png This script has not been tested in MATLAB See the individual file histories for the simpler MATLAB scripts that were the basis of this script Generation of svg files by minor modification of the script displayed visual artifacts and renderer incompatibilities that could not be easily fixed The current script fixes the visual artifacts in the png file as a post-processing step The script generates a semi-transparent grid by taking a weighted average of two images one with the grid and one without <source lang Matlab > function plotWindowLayer w N gridded wname wspecifier M 32; k 0 N-1; dr 120; H abs fft w zeros 1 M-1 N ; H fftshift H ; H H/max H ; H 20 log10 H ; H max -dr H ; figure 'Position' 1 1 1200 520 subplot 1 2 1 set gca 'FontSize' 28 area k w 'FaceColor' 0 1 1 'edgecolor' 1 1 0 'linewidth' 2 xlim 0 N-1 if min w > -0 01 ylim 0 1 05 set gca 'YTick' 0 0 1 1 ylabel 'amplitude' 'position' -16 0 525 0 else ylim -1 5 set gca 'YTick' -1 1 5 ylabel 'amplitude' 'position' -16 2 0 endif set gca 'XTick' 0 1/8 1 N-1 set gca 'XTickLabel' ' 0'; ' '; ' '; ' '; ' '; ' '; ' '; ' '; 'N-1' grid gridded set gca 'LineWidth' 2 set gca 'gridlinestyle' '-' xlabel 'samples' if strcmp wspecifier title cstrcat wname ' window' else title cstrcat wname ' window ' wspecifier ' ' endif set gca 'Position' 0 08 0 11 0 4 0 8 set gca 'XColor' 1 0 1 set gca 'YColor' 1 0 1 subplot 1 2 2 set gca 'FontSize' 28 h stem 1 M N-1-M N/2 /M H '-' ; set h 'BaseValue' -dr ylim -dr 6 set gca 'YTick' 0 -10 -dr set findobj 'Type' 'line' 'Marker' 'none' 'Color' 0 1 1 xlim -M N/2 M N/2/M grid gridded set findobj 'Type' 'gridline' 'Color' 871 49 0 set gca 'LineWidth' 2 set gca 'gridlinestyle' '-' ylabel 'decibels' xlabel 'bins' title 'Frequency response' set gca 'Position' 0 59 0 11 0 4 0 8 set gca 'XColor' 1 0 1 set gca 'YColor' 1 0 1 endfunction function plotWindow w wname wspecifier wfilespecifier if strcmp wfilespecifier wfilespecifier wspecifier; endif N size w 2 ; B N sum w 2 /sum w 2 noise bandwidth bins set N 4096 to get an accurate estimate plotWindowLayer w N on wname wspecifier ; print temp1 png -dpng -S2500 1165 close plotWindowLayer w N off wname wspecifier ; print temp2 png -dpng -S2500 1165 close I imread temp1 png ; J imread temp2 png ; info imfinfo temp1 png ; w info Width; c 1- double I 1 w/2 1 +2 double J 1 w/2 1 / 255 3 ; m 1- double I 1 w/2 2 +2 double J 1 w/2 2 / 255 3 ; y 1- double I 1 w/2 3 +2 double J 1 w/2 3 / 255 3 ; c c m c y c > 0 1-m-y ; I 1 w/2 1 255 1-c-m-y + 0 m + 0 y + 0 c ; I 1 w/2 2 255 1-c-m-y + 0 m + 0 y + 0 4 c ; I 1 w/2 3 255 1-c-m-y + 0 m + 0 y + 0 6 c ; c 1- double I w/2+1 w 1 +2 double J w/2+1 w 1 / 255 3 ; m 1- double I w/2+1 w 2 +2 double J w/2+1 w 2 / 255 3 ; y 1- double I w/2+1 w 3 +2 double J w/2+1 w 3 / 255 3 ; c c m c y c; I w/2+1 w 1 255 1-c-m-y + 0 m + 0 y + 0 8710 c ; I w/2+1 w 2 255 1-c-m-y + 0 m + 0 y + 0 49 c ; I w/2+1 w 3 255 1-c-m-y + 0 m + 0 y + 0 c ; if strcmp wfilespecifier imwrite I cstrcat 'Window function and frequency response - ' wname ' png' ; else imwrite I cstrcat 'Window function and frequency response - ' wname ' ' wfilespecifier ' png' ; endif endfunction N 128; k 0 N-1; w 0 42 - 0 5 cos 2 pi k/ N-1 + 0 08 cos 4 pi k/ N-1 ; plotWindow w Blackman w 0 355768 - 0 487396 cos 2 pi k/ N-1 + 0 144232 cos 4 pi k/ N-1 -0 012604 cos 6 pi k/ N-1 ; plotWindow w Nuttall continuous first derivative w 1 - 1 93 cos 2 pi k/ N-1 + 1 29 cos 4 pi k/ N-1 -0 388 cos 6 pi k/ N-1 +0 032 cos 8 pi k/ N-1 ; plotWindow w Flat top w 1 - 1 93 cos 2 pi k/ N-1 + 1 29 cos 4 pi k/ N-1 -0 388 cos 6 pi k/ N-1 +0 028 cos 8 pi k/ N-1 ; plotWindow w SRS flat top w ones 1 N ; plotWindow w Rectangular w N/2 - abs 0 N-1- N-1 /2 / N/2 ; plotWindow w Triangular w 0 5 - 0 5 cos 2 pi k/ N-1 ; plotWindow w Hann w 0 53836 - 0 46164 cos 2 pi k/ N-1 ; plotWindow w Hamming alpha 0 53836 alpha 0 5; w ones 1 N ; n - N-1 /2 -alpha N/2; L length n ; w 1 L 0 5 1+cos pi abs n -alpha N/2 / 1-alpha N/2 ; w N -1 N-L+1 w 1 L ; plotWindow w Tukey alpha 0 5 w sin pi k/ N-1 ; plotWindow w Cosine w sinc 2 k/ N-1 -1 ; plotWindow w Lanczos w N-1 /2 - abs 0 N-1- N-1 /2 / N-1 /2 ; plotWindow w Bartlett sigma 0 4; w exp -0 5 k- N-1 /2 / sigma N-1 /2 2 ; plotWindow w Gaussian sigma 0 4 w 0 62 -0 48 abs k/ N-1 -0 5 +0 38 cos 2 pi k/ N-1 -0 5 ; plotWindow w Bartlett “Hann alpha 2; w besseli 0 pi alpha sqrt 1- 2 k/ N-1 -1 2 /besseli 0 pi alpha ; plotWindow w Kaiser alpha 2 alpha 3; w besseli 0 pi alpha sqrt 1- 2 k/ N-1 -1 2 /besseli 0 pi alpha ; plotWindow w Kaiser alpha 3 tau N-1; epsilon 0 1; t_cut tau 0 5 - epsilon ; T_in abs k - 0 5 tau ; z_exp t_cut - 0 5 tau / T_in - t_cut + t_cut - 0 5 tau / T_in - 0 5 tau ; sigma T_in < 0 5 tau / exp z_exp + 1 ; w 1 T_in < t_cut + sigma T_in > t_cut ; plotWindow w Planck-taper epsilon 0 1 w 0 35875 - 0 48829 cos 2 pi k/ N-1 + 0 14128 cos 4 pi k/ N-1 -0 01168 cos 6 pi k/ N-1 ; plotWindow w Blackman-Harris w 0 3635819 - 0 4891775 cos 2 pi k/ N-1 + 0 1365995 cos 4 pi k/ N-1 -0 0106411 cos 6 pi k/ N-1 ; plotWindow w Blackman-Nuttall w 1 - 1 93 cos 2 pi k/ N-1 + 1 29 cos 4 pi k/ N-1 -0 388 cos 6 pi k/ N-1 +0 032 cos 8 pi k/ N-1 ; plotWindow w Flat top tau N/2 ; w exp -abs k- N-1 /2 /tau ; plotWindow w Exponential tau N/2 half window decay tau N/2 / 60/8 69 ; w exp -abs k- N-1 /2 /tau ; plotWindow w Exponential tau N/2 / 60/8 69 60dB decay alpha 2; w 1/2 1 - cos 2 pi k/ N-1 exp alpha abs N-2 k-1 / 1-N ; plotWindow w Hann-Poisson alpha 2 </source> Window function Images with Matlab source code | ||||