MAKE A MEME
View Large Image
| View Original: | Variations of the Fourier transform.tif (1536x1344) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
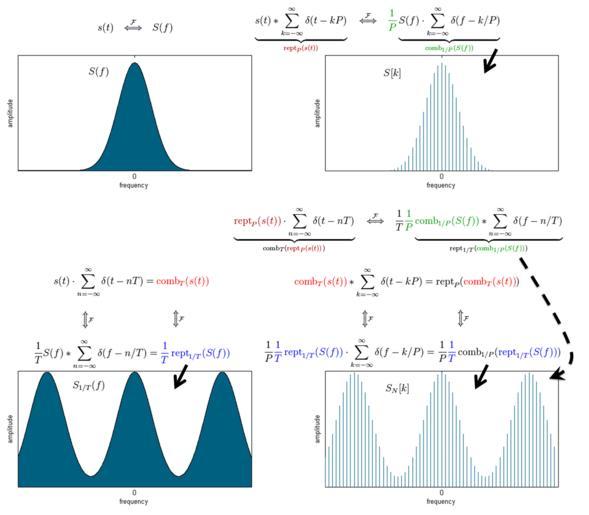
| Keywords: Variations of the Fourier transform.tif math Dirac comb functions and the convolution theorem to model the effects of sampling and/or periodic summation At lower left is a DTFT the spectral result of sampling s t at intervals of T The spectral sequences at a upper right and b lower right are respectively computed from a one cycle of the periodic summation of s t and b one cycle of the periodic summation of the s nT sequence The respective formulas are a the Fourier series <u>integral</u> and b the DFT <u>summation</u> The relative computational ease of the DFT sequence and the insight it gives into S f make it a popular analysis tool 2011-12-13 own Bob K https //commons wikimedia org/wiki/File Fourier_transform _Fourier_series _DTFT _DFT gif Matlab commands <source lang Matlab > N 1024; x -N/2 N/2-1; 1xN y exp -0 1 x 2 ; 1xN z exp -0 8 x 2 ; 1xN Y fftshift abs fft y zeros 1 7 N ; W exp j 2 pi/ 3 N x' -4 N 4 N-1 ; Nx1 1x8N Z abs z W ; 1xN Nx8N figure subplot 2 2 1 area -4 N 4 N-1 Y 'FaceColor' 0 4 6 xlim -4 N 4 N-1 ; set gca 'XTick' 0 set gca 'YTick' ylabel 'amplitude' xlabel 'frequency' subplot 2 2 3 area -4 N 4 N-1 Z 'FaceColor' 0 4 6 xlim -4 N 4 N-1 ; set gca 'XTick' 0 set gca 'YTick' ylabel 'amplitude' xlabel 'frequency' Y1 zeros 1 8 N ; Y1 1 128 end Y 1 128 end ; subplot 2 2 2 stem -4 N 4 N-1 Y1 '-' 'Color' 0 4 6 ; set findobj 'Type' 'line' 'Marker' 'none' xlim -4 N 4 N-1 ; set gca 'XTick' 0 set gca 'YTick' ylabel 'amplitude' xlabel 'frequency' Z1 zeros 1 8 N ; Z1 1 128 end Z 1 128 end ; subplot 2 2 4 stem -4 N 4 N-1 Z1 '-' 'Color' 0 4 6 ; set findobj 'Type' 'line' 'Marker' 'none' xlim -4 N 4 N-1 ; set gca 'XTick' 0 set gca 'YTick' ylabel 'amplitude' xlabel 'frequency' </source> LaTex <math>s t \quad\stackrel \mathcal F \Longleftrightarrow \quad S f \ </math> <math>Sk \quad S_ 1/T f \quad S_Nk\ </math> <math>\underbrace s t \sum_ k -\infty \infty \delta t-kP _ \color BrickRed \operatorname rept _P s t \quad\stackrel \mathcal F \Longleftrightarrow \quad \color OliveGreen \frac 1 P \underbrace S f \cdot \sum_ k -\infty \infty \delta f-k/P _ \color OliveGreen \operatorname comb _ 1/P S f \ </math> <math>\underbrace s t \cdot \sum_ n -\infty \infty \delta t-nT _ \operatorname comb _T s t \quad\stackrel \mathcal F \Longleftrightarrow \quad \frac 1 T \underbrace S f \sum_ n -\infty \infty \delta f-n/T _ \operatorname rept _ 1/T S f \ </math> <math>s t \cdot \sum_ n -\infty \infty \delta t-nT \color Red \operatorname comb _T s t \ </math> <math>\frac 1 T S f \sum_ n -\infty \infty \delta f-n/T \color Blue \frac 1 T \operatorname rept _ 1/T S f \ </math> <math>\underbrace \color BrickRed \operatorname rept _P s t \cdot \sum_ n -\infty \infty \delta t-nT _ \operatorname comb _T \color BrickRed \operatorname rept _P s t \quad\stackrel \mathcal F \Longleftrightarrow \quad \frac 1 T \color OliveGreen \frac 1 P \underbrace \color OliveGreen \operatorname comb _ 1/P S f \sum_ n -\infty \infty \delta f-n/T _ \operatorname rept _ 1/T \color OliveGreen \operatorname comb _ 1/P S f </math> <math>\underbrace \operatorname comb _T s t \sum_ k -\infty \infty \delta t-kP _ \operatorname rept _P \operatorname comb _T s t \quad\stackrel \mathcal F \Longleftrightarrow \quad \frac 1 P \frac 1 T \underbrace \operatorname rept _ 1/T S f \cdot \sum_ k -\infty \infty \delta f-k/P _ \operatorname comb _ 1/P \operatorname rept _ 1/T S f </math> <math> \color Red \operatorname comb _T s t \sum_ k -\infty \infty \delta t-kP \operatorname rept _P \color Red \operatorname comb _T s t </math> <math>\frac 1 P \color Blue \frac 1 T \operatorname rept _ 1/T S f \cdot \sum_ k -\infty \infty \delta f-k/P \frac 1 P \color Blue \frac 1 T \operatorname comb _ 1/P \color Blue \operatorname rept _ 1/T S f </math> cc-zero Uploaded with UploadWizard Fourier analysis Digital signal processing Amplitude | ||||