MAKE A MEME
View Large Image
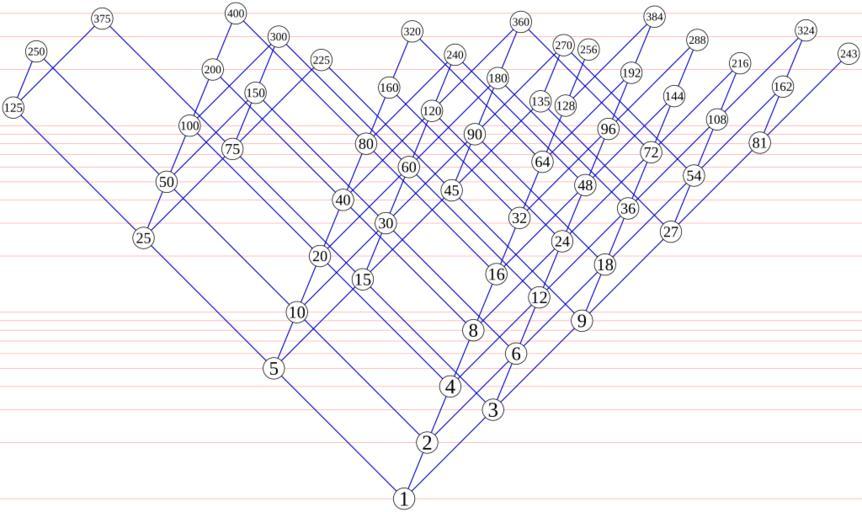
| View Original: | Regular divisibility lattice.svg (1363x809) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Regular divisibility lattice.svg A Hasse diagram of divisibility relationships among regular numbers up to 400 As shown by the horizontal light red lines the vertical position of each number is proportional to its logarithm Inspired by similar diagrams in a paper by Kurenniemi http //www beige org/projects/dimi/CSDL2 pdf en wikipedia 2007-03-14 David Eppstein wikipedia en David Eppstein Source code The Python source code for generating this image <pre> from math import log limit 400 radius 17 margin 4 xscale yscale 128 skew 0 285 def A051037 yield 1 seq 1 spiders 2 2 0 0 3 3 0 1 5 5 0 2 while True x p i j min spiders if x seq-1 yield x seq append x spidersj p seqi+1 p i+1 j def nfactors h p nf 0 while h p 0 nf + 1 h // p return nf seq for h in A051037 if h > limit break seq append h nfactors h 2 nfactors h 3 nfactors h 5 leftmost max k for h i j k in seq rightmost max j for h i j k in seq leftwidth int 0 5 + log 5 leftmost xscale + radius + margin rightwidth int 0 5 + log 3 rightmost xscale + radius + margin width leftwidth + rightwidth height int 0 5 + log limit yscale + 2 radius + margin def place h i j k logical coordinates x j log 3 - k log 5 + i skew y log h physical coordinates x x xscale + leftwidth y -y yscale + height - radius - margin return x y print < xml version 1 0 encoding utf-8 > < DOCTYPE svg PUBLIC -//W3C//DTD SVG 1 1//EN http //www w3 org/Graphics/SVG/1 1/DTD/svg11 dtd > <svg xmlns http //www w3 org/2000/svg version 1 1 width d height d > width height print ' <g style fill none;stroke ffaaaa; >' l 1 base 1 while l < limit y -yscale log l + height - radius - margin print ' <path d M0 0 2fL d 0 2f />' y width y l + base if l 10 base base l print </g> print ' <g style fill none;stroke-width 1 5;stroke 0000cc; >' def drawSegment p q x1 y1 p x2 y2 q print ' <path d M 0 2f 0 2fL 0 2f 0 2f />' x1 y1 x2 y2 for h i j k in seq x y place h i j k if i > 0 drawSegment place h//2 i-1 j k x y if j > 0 drawSegment place h//3 i j-1 k x y if k > 0 drawSegment place h//5 i j k-1 x y print </g> print ' <g style fill ffffff;stroke 000000; >' for h i j k in seq x y place h i j k print ' <circle cx 0 2f cy 0 2f r d />' x y radius pairs of first value with size size of that value fontsizes 1 33 5 30 10 27 20 24 100 20 200 18 for h i j k in seq x y place h i j k if h in fontsizes print </g> print ' <g style font-family Times;font-size d;text-anchor middle; >' fontsizesh lower fontsizesh / 3 print ' <text x 0 2f y 0 2f > d</text>' x y+lower h print </g> print </svg> </pre> original upload log page en wikipedia Regular_divisibility_lattice svg 2007-03-14 05 08 David Eppstein 1363×809×0 13167 bytes <nowiki>A Hasse diagram of divisibility relationships among regular numbers up to 400 Inspired by similar diagrams in a paper by Kurenniemi http //www beige org/projects/dimi/CSDL2 pdf </nowiki> Files by User David Eppstein from en wikipedia Divisibility lattice Hasse diagrams Images with Python source code | ||||