MAKE A MEME
View Large Image
| View Original: | Midpoint method illustration.png (1863x1667) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
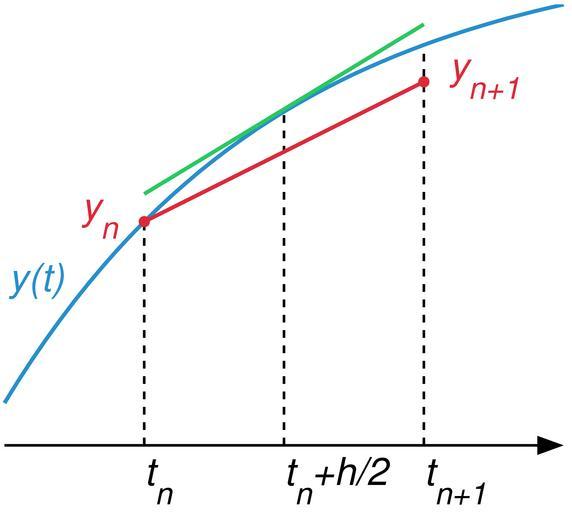
| Keywords: Midpoint method illustration.png Illustration of Midpoint method own Oleg Alexandrov Created with MATLAB Source code MATLAB <source lang matlab > illustration of numerical integration compare the Forward Euler method which is globally O h with Midpoint method which is globally O h 2 and the exact solution function main f inline '2-y' 't' 'y' ; will solve y' f t y a 0; b 1; endpoints of the interval where we will solve the ODE A -0 5 b; B 1 5 b; a bit of an expanded interval N 2; T linspace a b N ; h T 2 -T 1 ; the grid y0 1; initial condition One step of the midpoint method Y solve_ODE N f y0 h T 2 ; midpoint method exact solution to the right hh 0 05; TT a hh B; NN length TT ; YY solve_ODE NN f y0 hh TT 2 ; midpoint method exact solution to the left TTl a hh -A ; NN length TTl ; ZZ solve_ODE NN f y0 -hh TTl 2 ; midpoint method the tangent line at the midpoint tmid a+b /2; I find TT > tmid ; m I 1 ; tmid TT m ; ymid YY m ; slope f tmid ymid ; Tan_l 0 5 b; Tant tmid-Tan_l hh tmid+Tan_l ; Tany slope Tant-tmid +ymid; prepare the plotting window lw 3; curves linewidth lw_thin 2; thinner curves fs 30; font size figure 1 ; clf; hold on; axis equal; axis off; colors red 0 867 0 06 0 14; blue 0 129 205/256; green 0 200 70/256; black 0 0 0; coordinate axes shifty 0 2; arrowsize 0 1; arrow_type 1; angle 20; in degrees arrow A shifty B shifty lw_thin arrowsize angle arrow_type black plot auxiliary lines I find TT > a ; m I 1 ; ya YY m ; plot a a 0+shifty ya 'linewidth' lw_thin 'linestyle' '--' 'color' black I find TT > tmid ; m I 1 ; ymid YY m ; plot tmid tmid 0+shifty ymid 'linewidth' lw_thin 'linestyle' '--' 'color' black I find TT > b ; m I 1 ; yb YY m ; plot b b 0+shifty yb 'linewidth' lw_thin 'linestyle' '--' 'color' black plot the solutions plot TT YY 'color' blue 'linewidth' lw ; plot -TTl ZZ 'color' blue 'linewidth' lw plot T Y 'color' red 'linewidth' lw plot the tangent line plot Tant Tany+0 003 lw 'color' green 'linewidth' lw smallrad 0 02; ball T 1 Y 1 smallrad red ball T length T Y length Y smallrad red text small 0 15; text a shifty-small '\it t_n ' 'fontsize' fs text tmid shifty-small '\it t_n+h/2 ' 'fontsize' fs text b shifty-small '\it t_ n+1 ' 'fontsize' fs text T 1 -1 5 small Y 1 '\it y_n ' 'fontsize' fs 'color' red text T length T +0 6 small Y length Y '\it y_ n+1 ' 'fontsize' fs 'color' red text -TTl length TTl +0 1 small ZZ length ZZ +3 small '\it y t ' 'fontsize' fs 'color' blue axes aspect ratio pbaspect 1 1 5 1 ; save to disk saveas gcf sprintf 'Midpoint_method_illustration eps' h 'psc2' ; function Y solve_ODE N f y0 h T method Y 0 T; Y 1 y0; for i 1 N-1 t T i ; y Y i ; if method 1 forward Euler method Y i+1 y + h f t y ; elseif method 2 explicit one step midpoint method K y + 0 5 h f t y ; Y i+1 y + h f t+h/2 K ; else disp 'Don`t know this type of method' ; return; end end function arrow start stop thickness arrow_size sharpness arrow_type color Function arguments start stop start and end coordinates of arrow vectors of size 2 thickness thickness of arrow stick arrow_size the size of the two sides of the angle in this picture -> sharpness angle between the arrow stick and arrow side in degrees arrow_type 1 for filled arrow otherwise the arrow will be just two segments color arrow color a vector of length three with values in 0 1 convert to complex numbers i sqrt -1 ; start start 1 +i start 2 ; stop stop 1 +i stop 2 ; rotate_angle exp i pi sharpness/180 ; points making up the arrow tip besides the stop point point1 stop - arrow_size rotate_angle stop-start /abs stop-start ; point2 stop - arrow_size/rotate_angle stop-start /abs stop-start ; if arrow_type 1 filled arrow plot the stick but not till the end looks bad t 0 5 arrow_size cos pi sharpness/180 /abs stop-start ; stop1 t start+ 1-t stop; plot real start stop1 imag start stop1 'LineWidth' thickness 'Color' color ; fill the arrow H fill real stop point1 point2 imag stop point1 point2 color ; set H 'EdgeColor' 'none' else two-segment arrow plot real start stop imag start stop 'LineWidth' thickness 'Color' color ; plot real stop point1 imag stop point1 'LineWidth' thickness 'Color' color ; plot real stop point2 imag stop point2 'LineWidth' thickness 'Color' color ; end function ball x y r color Theta 0 0 1 2 pi; X r cos Theta +x; Y r sin Theta +y; H fill X Y color ; set H 'EdgeColor' 'none' ; </source> Images with Matlab source code Numerical analysis Files by User Oleg Alexandrov from en wikipedia math | ||||