MAKE A MEME
View Large Image
| View Original: | L-Verzahnung.png (488x400) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
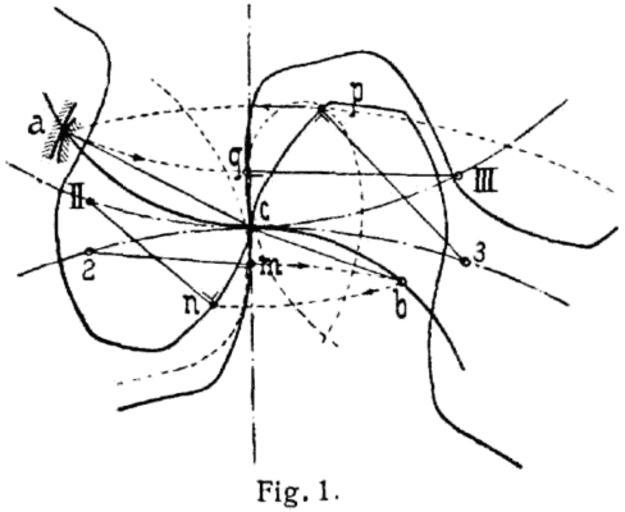
| Keywords: L-Verzahnung.png de Verzahnungen bewirken an Zahnradgetrieben Kraft- und Bewegungsübertragung in Kapselwerken Abdichtung gegen Rückströmung Sollen zwei Zahnräder Fig 1 im allgemeinen Fall mit gleichmäßiger Geschwindigkeitsübertragung nämlich so zusammenarbeiten daß ihre Teilkreise abrollen ohne zu gleiten so muß sich in jedem Augenblick das eine Rad relativ zum andern derart bewegen daß es sich um den augenblicklichen Berührungspunkt c der Teilkreise dreht Wenn nun an beliebiger Stelle z B in a zwei Zahnflanken beider Räder sich berühren so müssen sich auch diese augenblicklich um c drehend bewegen d h die Berührung muß normal zu a c stattfinden Darum kann ein Zahnflankenstück nur in solcher Stellung richtig arbeiten bei welcher seine Normale durch c geht So wird der Punkt p zum Eingriff kommen wenn die auf der Zahnflanke in p errichtete Normale p 3 sich mit dem unteren Rade so weit gedreht hat daß 3 nach c gekommen ist wobei a c p 3 ist Hierdurch ist ein Punkt a der Eingrifflinie bestimmt Die Linie ac ist beiden Rädern augenblicklich gemeinsam Dreht man nun das obere Rad mit seiner Linie a c um das Bogenstück c III c 3 zurück so kommt ac nach q III und die Zahnflanke in q muß normal zu q III verlaufen Ebenso kommen die Punkte m und n in b zum Eingriff während die beiden Normalen m 2 und n II zugleich nach b c gekommen sind Nach diesem von Reuleaux angegebenen Verfahren der allgemeinen Verzahnung kann man zu einer gegebenen Zahnform vorausgesetzt daß deren Normalen den Teilkreis schneiden die Eingrifflinie und die zugehörige Zahnform ableiten Die Richtung von c nach einem Punkte der Eingrifflinie gibt die Krastrichtung ohne Rücksicht auf die Zahnflankenreibung an Die Systeme sind durch die Form der Eingrifflinie bestimmt Die fast ausschließlich benutzte Evolventenverzahnung Bd 3 S 520 hat eine geradlinige Eingrifflinie die schräg durch den Berührungspunkte der Teilkreise T geht in der Regel mit der Neigung ß 75° nach amerikanischem Gebrauch mit 711/2° oder tg ß 3 Die die Gerade berührenden Grundkreise G sind im Verhältnis sin ß kleiner als die Teilkreise Bei der Abwicklung der Geraden auf einem ihrer Grundkreise beschreibt jeder Punkt eine Evolvente als Zahnkurve die nur nach der Größe der Grundkreise verschieden ausfällt Für die Zahnstange mit unendlich entferntem Grundkreise geht sie in eine zur Eingrifflinie senkrecht stehende gerade Linie über Fig 2 Bei Hohlrädern wird die Zahnflanke konkav Fig 3 Zur Aufzeichnung 6 der Evolvente trägt man nach Bd 3 S 520 Fig 1 auf der Geraden und dem Lexikon Verzahnungen Lueger Lexikon der gesamten Technik S 39705 vgl Lueger Bd 8 S 791 ff Lueger Lueger/Machine elements Drawings of gears and gearboxes Gear tooth design | ||||