MAKE A MEME
View Large Image
| View Original: | Integer multiplication by FFT.svg (665x579) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
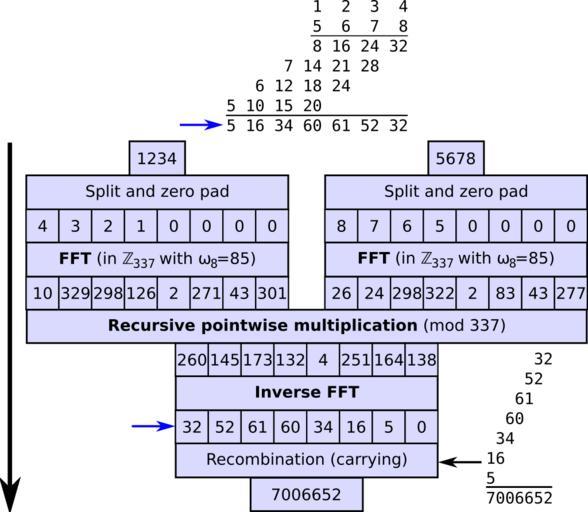
| Keywords: Integer multiplication by FFT.svg en A demonstration of an integer multiplication based on fast Fourier transforms FFTs using a number theoretic transform in the finite field of order 337 choosing 85 as an 8th root of unity since the input vectors are of length 8 Base 10 is used normally a power of 2 would used but 10 is convenient for demonstration and this technique is overkill for integers of this size long multiplication would be superior Because the inputs have 4 digits and the maximum product of two digits in base 10 is 9<sup>2</sup> the base was chosen as the first prime p greater than 4×9<sup>2</sup> 324 where 8 is invertible in the integers modulo p in this example any suitable base > 61 such as 73 would suffice but we don't know that a priori The computation at the top shows how the same acyclic convolution can be computed naively by long multiplication without carrying showing the relationship to multiplication The computation in the lower right shows recombination/carrying of the result vector by decimal shifts and adds to obtain the final integer result Note that all recursive multiplications are of smaller 3-digit integers Values are all accurate and were computed using the following Mathematica code <pre> NTTx_ b_ r_ TableModSumxn + 1 PowerModr k n b n 0 Lengthx - 1 b k 0 Lengthx - 1 INTTx_ b_ r_ Block ninverse ninverse PowerModLengthx -1 b; TableMod ninverse Sumxn + 1 PowerModr Lengthx - n k b n 0 Lengthx - 1 b k 0 Lengthx - 1 x 4 3 2 1 0 0 0 0 ; y 8 7 6 5 0 0 0 0 ; b 337; r 85; NTTx b r NTTy b r ModNTTx b r NTTy b r b INTTModNTTx b r NTTy b r b b r 1234 5678 </pre> 2011-12-17 own Dcoetzee cc-zero Uploaded with UploadWizard Multiplication | ||||