SnappyGoat.com - Free Public Domain Images - SnappyGoat.com- Implicit Function Theorem.svg

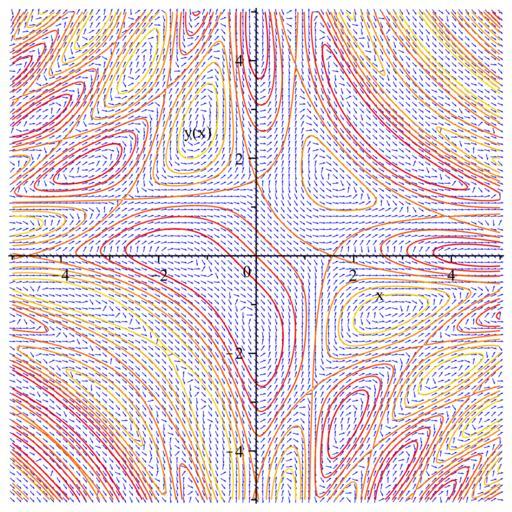
MAKE A MEME View Large Image $Implicit Function Theorem.svg Demonstration of the Implicit Function Theorem The curves are the implicitly defined as <math>f x y \sin x+y -\cos xy C</math> with various values of the constant <math>C</math> The background slope field shows ...$

View Original:	Implicit Function Theorem.svg (556x556)
Download:	Original	Medium	Small	Thumb
Courtesy of:	commons.wikimedia.org			More Like This
Keywords: Implicit Function Theorem.svg Demonstration of the Implicit Function Theorem The curves are the implicitly defined as <math>f x y \sin x+y -\cos xy C</math> with various values of the constant <math>C</math> The background slope field shows that if one is given a point on the curve then one can in principle generate a local piece of the curve defined as an explicit function of x or at least approximate it by tracing from slope field e g approximation by Euler's method which can be made as accurate as desired by choosing small step size; as step size approaches zero the result matches the actual local piece of curve more accurately Own 2008-05-08 Saran T Vector fields Implicit curves