MAKE A MEME
View Large Image
| View Original: | HornerandNewton.gif (500x350) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
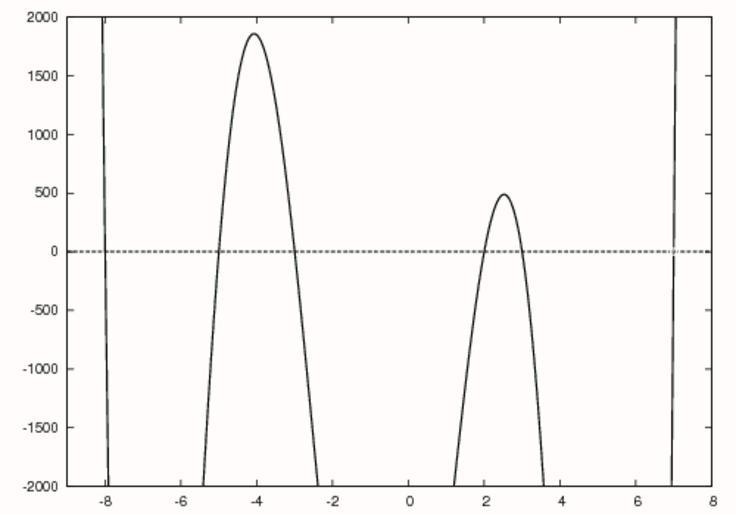
| Keywords: HornerandNewton.gif pt Gif mostrando como encontrar raízes de um polinômio usando o método de Newton para aproximar as raízes e o método de horner para fazer deflexões no polinômio en Animation demonstrating how to find the roots of a polynomial using Newton's method and Horner's method together own Philten wikipedia en 2009-05-20 Philten graph Source Made using GNU Octave and compiled with the GIMP <source lang matlab > clear epsilon 0 01; a 1 4 -72 -214 1127 1602 -5040; color 0 0 0; 255 0 0; 255 255 0; 0 255 0; 0 0 255; 255 0 255/255; grad fliplr 0 0 1 1 0 0 1 1; xlim -9 8; ylim -2000 2000; x0 10; x xlim 1 01 xlim 2 ; roots 1 newton a x0 epsilon ; b a; for i 2 length a -1 y a horner b i-1 roots i-1 ; b i 0 a; roots i newton b i roots i-1 epsilon ; endfor b length a b 1 ; for i 1 length a fancy graphics for j 1 length grad shade grad j 1 1 1-color i ; hold off plot x polyval b i x 'color' color i +shade 'linewidth' 3 hold on plot x polyval b 1 x 'color' color 1 'linewidth' 3 plot x zeros size x '--k' 'linewidth' 3 for k 1 i-1 plot roots k 0 'o' 'color' color k 'markersize' 1 'linewidth' 3 endfor if j < length grad /2 plot roots i 0 'o' 'color' color i +shade 'markersize' 1 'linewidth' 3 else plot roots i 0 'o' 'color' color i 'markersize' 1 'linewidth' 3 endif axis xlim ylim print strcat frame num2str j+length grad i-1 eps endfor endfor </source> <source lang matlab > function z newton a x0 epsilon x1 epsilon 2+x0; loops 0; for i 1 length a -1 b i a i length a -i ; endfor while abs x0-x1 > epsilon loops < 500 x0 x1; f horner a x0 ; fp horner b x0 ; x1 x0 - f/fp; loops++; endwhile z x1; endfunction </source> <source lang matlab > function y b horner a x b 1 a 1 ; for i 2 length a b i a i +x b i-1 ; endfor y b length a ; b b 1 length b -1 ; endfunction </source> Original upload log page en wikipedia HornerScheme gif 2009-05-20 01 30 Philten 500×350× 871553 bytes <nowiki>made using GNU Octave and compiled with the GIMP clear epsilon 0 01; a 1 4 -72 -214 1127 1602 -5040; color 0 0 0; 255 0 0; 255 255 0; 0 255 0; 0 0 255; 255 0 255/255; grad fliplr 0 0 1 1 0 0 1 1; xlim -9 8; ylim -2000 2000; </nowiki> Uncategorized 2013 May 27 | ||||