MAKE A MEME
View Large Image
| View Original: | Golden Ratio. Deriving equation.svg (216x377) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
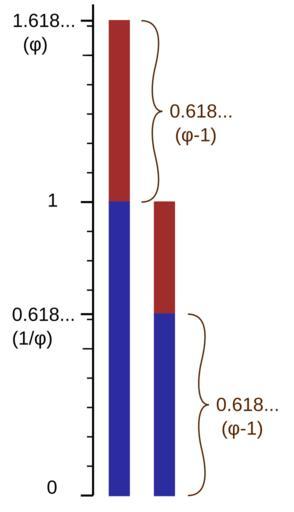
| Keywords: Golden Ratio. Deriving equation.svg en Caption This image illustrates why 1/φ φ-1<br />Using the image on the right it can be visually appreciated although with difficulty that inverse of the golden ratio equals the golden ratio minus one or 1/φ φ-1 To see this mathematical relationship in the animation first imagine a vertical number line where the bottom of all the bars are at the number line ™s origin or point 0 Also imagine that the top of the first blue bar is at the point 1 on the number line That would make the top of the first red bar coincide with the point 1 618 which is the golden ratio Since the length of the first blue bar is 1 that makes the length of the first red bar equal to 0 618 or φ-1 which is the right hand side of the equation we are discussing 1/φ φ-1 Now first note that two numbers are multiplicative inverses if when they are multiplied together you get 1 In our instance this means φ 1/φ 1 and we want to show that 1/φ φ-1 It is a direct mathematical fact that if the top of the first blue bar is at the point 1 and the second composite bar has the same red to blue ratio as the first then the top of the second blue bar corresponds to the point on the number line that is the inverse of the point at the top of the first red bar This is a general fact and is not specific to the golden ratio however since the top of the first red bar is at φ 1 618 then the top of the second blue bar is at 1/φ And finally since the length of the second blue bar is equal to the length of the first red bar 1/φ φ-1 Golden Ratio Display Animation gif Golden Ratio Variation Animation gif Golden ratio | ||||