MAKE A MEME
View Large Image
| View Original: | Displacement current in capacitor.svg (744x800) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
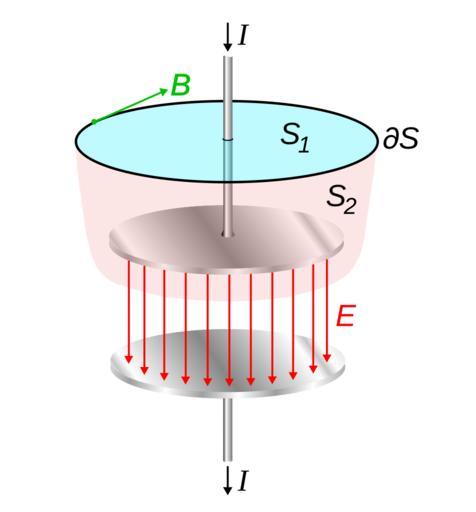
| Keywords: Displacement current in capacitor.svg Diagram of a widely used example demonstrating need for the displacement current term in Maxwell's equations The diagram shows a capacitor being charged by current <math>I\ </math> flowing through a wire which creates a magnetic field <math>\mathbf B \ </math> around it The magnetic field is found from Ampere's law <math>\oint_ \partial S \mathbf B \cdot d\mathbf l \mu_0 \int_S \mathbf J + \epsilon_0 \frac \partial \mathbf E \partial t \cdot d\mathbf S \ </math> The equation says that the integral of the magnetic field <math>\mathbf B \ </math> around a loop <math>\partial S\ </math> is equal to the current <math>\mathbf J \ </math> through any surface spanning the loop plus a term depending on the rate of change of the electric field <math>\mathbf E \ </math> through the surface This term the second term on the right is the displacement current For applications with no time varying electric fields unchanging charge density it is zero and is ignored However in applications with time varying fields such as circuits with capacitors it is needed as shown below Any surface intersecting the wire such as <math>S_1\ </math> has current <math>I\ </math> passing through it so Ampere's law gives the correct magnetic field <math>B \frac \mu_0 I 2 \pi r \ </math> But surface <math>S_2\ </math> spanning the same loop that passes between the capacitor's plates has no current flowing through it so without the displacement current term Ampere's law gives <math>B 0\ </math> So without the displacement current term Ampere's law fails; it gives different results depending on which surface is used which is inconsistent The 'displacement current' term provides a second source for the magnetic field besides current; the rate of change of the electric field <math>\mathbf E \ </math> Between the capacitor's plates the electric field is increasing so the rate of change of electric field through the surface <math>S_2\ </math> is positive and its magnitude gives the correct value for the field field <math>\mathbf B \ </math> found above James Clerk Maxwell added the displacement current term to Ampere's law around 1861 Example taken from http //www feynmanlectures info/ Feynman Richard; Robert Leighton; Matthew Sands 1964 The Feynman Lectures on Physics Vol 2 Addison-Wesley USA p 18-4 using slightly different terminology Own 2008-11-10 Chetvorno I Chris Burks Chetvorno the author release this work into the public domain for any use whatever Field diagrams James Clerk Maxwell Electric current | ||||