MAKE A MEME
View Large Image
| View Original: | DFT approximation to Hilbert filter.png (665x523) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
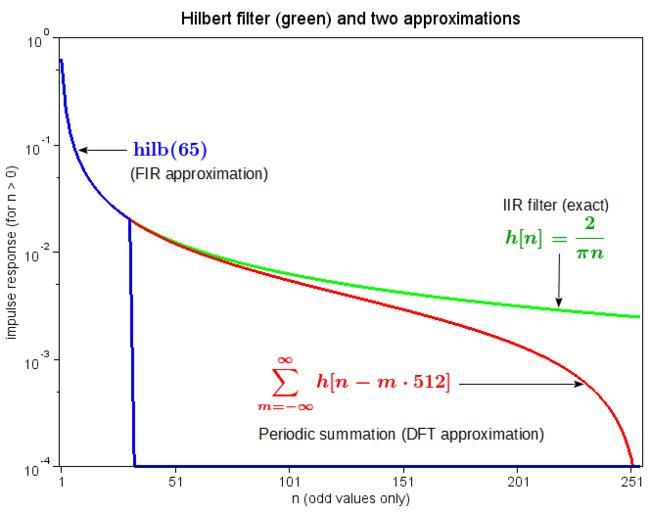
| Keywords: DFT approximation to Hilbert filter.png The green graph is a section of the infinitely long Hilbert transform filter impulse response The blue graph is a shorter section produced by the Scilab function hilb for use as an FIR filter hilb apparently just applies a simple rect window but other windows are also possible When the filtering convolution is performed by multiplication of DFTs in the frequency domain circular convolution people sometimes replace the DFT of hilb with samples of the DTFT discrete-time Fourier transform of hn 2/ Ï n whose real and imaginary components are all just 0 or ±1 thereby avoiding actual multiplications But in that case the convolution is actually being done with the periodic summation of hn shown in red Unlike hilb it never goes to zero which means that the edge effects of circular convolution affect distort every output sample They can't simply be eliminated by discarding a few corrupted samples That effect is generally worse than the distortion caused by windowing the hn sequence even with the crude rectangular window example own 2007-09-27 Bob K Scilab script <source lang Scilab > N 256; // length of plots // Create a seqment of the IIR filter h_IIR zeros 1 N ; odd 1 2 N; for n odd h_IIR n 2/ pi n ; end // Create another filter by sampling the DTFT H_DFT i 0 -ones 1 N-1 ones 1 N ; h_DFT real fft H_DFT 1 ; // inverse FFT h_DFT h_DFT 2 ; // align with h_IIR // Create a 65-tap FIR Hilbert transform filter M 65; h_65 hilb M ; M2 M-1 /2; h_65 h_65 M/2+2 M zeros 1 N- M2-1 ; // align with other filters // Display the results r 5; g 3; b 2; // based on a call to getcolor plot2d odd' h_IIR odd ' h_DFT odd ' h_65 odd ' logflag nl style g r b rect 0 0 0001 256 1 frameflag 1 axesflag 1 ; title Hilbert filter green and two approximations fontsize 4 ; ylabel impulse response for n > 0 fontsize 3 ; xlabel n odd values only fontsize 3 ; f gcf ; a gca ; //a box on ; included in frameflag 1 a font_size 3; //set the tics label font size a x_ticks tlist ticks locations labels 1 51 101 151 201 251 1 51 101 151 201 251 ; f children 1 children children thickness 3; // Can do it this way when the thicknesses are not all the same // pb a children children 1 ; // Note that the order compared to style is LIFO // pr a children children 2 ; // pg a children children 3 ; // pg thickness 3; // pr thickness 3; // equivalent to set pr 'thickness' 3 ; // pb thickness 3; </source> LaTex <math>\color OliveGreen \boldsymbol hn \frac 2 \pi n </math> <math>\color Blue \boldsymbol \operatorname hilb 65 </math> <math>\color Red \boldsymbol \sum_ m -\infty \infty hn - m\cdot 512 </math> La bildo estas kopiita de wikipedia en La originala priskribo estas 1 date/time username edit summary source ---- 23 55 7 December 2005 en User Bob K <nowiki> I created this image myself using Matlab tools </nowiki> http //en wikipedia org/wiki/Image DFT_approximation_to_Hilbert_filter png en Image DFT approximation to Hilbert filter png Signal processing | ||||