MAKE A MEME
View Large Image
| View Original: | Chain homotopy.svg (322x85) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
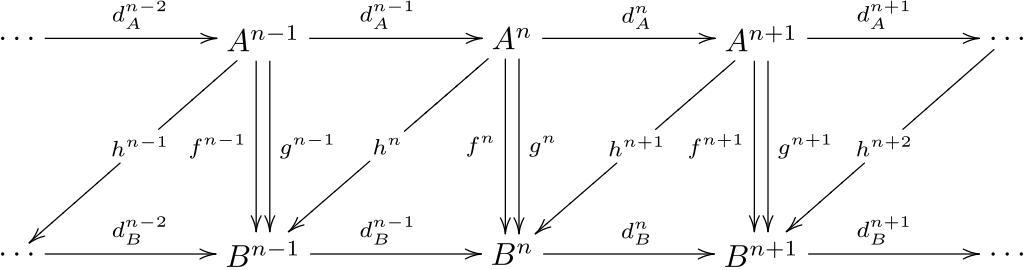
| Keywords: Chain homotopy.svg LaTeX source <pre> \documentclass amsart \usepackage amsmath amssymb nopageno \usepackageall xy \begin document \begin equation \xymatrix +3em \dots \arr d_A n - 2 A n - 1 \arr d_A n - 1 \ar <0 5ex>d g n - 1 \ar <-0 5ex>d_ f n - 1 \ardl +<1ex 1ex> \scriptstyle h n - 1 A n \arr d_A n \ar <0 5ex>d g n \ar <-0 5ex>d_ f n \ardl +<1ex 1ex> \scriptstyle h n A n + 1 \arr d_A n + 1 \ar <0 5ex>d g n + 1 \ar <-0 5ex>d_ f n + 1 \ardl +<1ex 1ex> \scriptstyle h n + 1 \dots \ardl +<1ex 1ex> \scriptstyle h n + 2 \\ \dots \arr d_B n - 2 B n - 1 \arr d_B n - 1 B n \arr d_B n B n + 1 \arr d_B n + 1 \dots \end equation \end document </pre> Let A be an additive category The homotopy category K A is based on the following definition if we have complexes A B and maps f g from A to B a chain homotopy from f to g is a collection of maps <math>h n \colon A n \to B n - 1 </math> not a map of complexes such that <math>f n - g n d_B n - 1 h n + h n + 1 d_A n </math> or simply <math> f - g d_B h + h d_A </math> This can be depicted as shown in the diagram en Image Chain homotopy jpg 2007-03-19 2008-02-06 en User Ryan Reich User Stannered Ryan Reich en Image Chain homotopy jpg Homological algebra Mathematical diagrams Images with LaTeX source code | ||||