MAKE A MEME
View Large Image
| View Original: | Brunnian-L10a140.svg (405x800) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
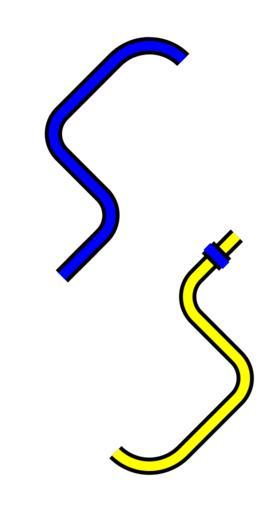
| Keywords: Brunnian-L10a140.svg Link http //katlas math toronto edu/wiki/L10a140 L10a140 of mathematical knot theory presented in a visual form which makes it evident that it is a Brunnian link The red loop is obviously not linked with either the blue or yellow loops and if the red loop were absent then the blue and yellow loops could also be separated from each other by tucking the big end of the blue loop into the yellow loop and the big end of the yellow loop into the blue loop Self-made graphic declared to be in public domain converted from the following PostScript source code <pre> 306 396 translate/X 1800 sqrt def /A 0 X 4 mul 711 sub 50 45 135 arc -70 X 3 mul 30 135 225 arc -70 X 30 45 -45 arcn -70 X neg 30 135 225 arc 0 X -3 mul 711 add 20 225 315 arc 70 X neg 30 -45 45 arc 70 X 30 225 135 arcn 70 X 3 mul 30 315 45 arc closepath gsave 18 setlinewidth 0 setgray stroke grestore 10 setlinewidth stroke def 0 0 1 setrgbcolor A gsave 1 1 0 setrgbcolor 180 rotate A grestore 1 0 0 setrgbcolor -70 -182 70 180 360 arc -70 182 70 0 180 arc closepath gsave 18 setlinewidth 0 setgray stroke grestore 10 setlinewidth stroke 18 setlinewidth 0 setgray -79 -9 moveto 18 18 rlineto stroke 79 -9 moveto -18 18 rlineto stroke 0 X 4 mul 711 sub 50 90 113 arc stroke 0 X -3 mul 711 add 20 240 300 arc stroke 10 setlinewidth 0 0 1 setrgbcolor -80 -10 moveto 20 20 rlineto stroke 80 -10 moveto -20 20 rlineto stroke 0 X 4 mul 711 sub 50 86 117 arc stroke 0 X -3 mul 711 add 20 236 304 arc stroke showpage EOF</pre> April-May 2013 AnonMoos L10a140 links Images with PostScript source code Outline knots and links Knots and links on transparent background | ||||